Table of Contents
Geometrical Optics PHYS143
(Updated April 2025)
This lab is intended to illustrate how light rays behave in some simple optical setups. The basic principles you will become familiar with in this lab are commonly encountered in many research applications ranging from quantum optics to telescopes. As part of this lab you will learn:
- How light of different wavelengths behaves at the boundary between two media with different optical densities.
- How to use lasers to test and verify the optical properties of materials using ray tracing techniques.
- How simple lenses can be used to form images.
- The basic principles of how telescope optics work.
- How to use simple lenses to build a telescope and measure it's magnification factor.
Introduction
The term geometrical optics refers to the study of light propagation in the limit as the wavelength of light is much smaller than any of the optical components of the system, e.g., apertures, lenses, or mirrors. Another simplifying assumption is that each medium through which the light travels (e.g., air, water, glass) is homogeneous and that all changes between media are abrupt at the interfaces. A consequence of these assumptions is that light travels in straight lines through each medium and that changes in the direction the light travels occur only at the interfaces between media. The direction light travels is conveniently described by the term rays.
Lab notebook template
One member of the group should click on the link below to start your group lab notebook. (You may be asked to log into your UChicago Google account if you are not already logged in.) Make sure to share the document with everyone in the group (click the “Share” button in the top right corner of the screen) so each member has access to the notebook after you leave lab. Choose one member of your group to be the designated record-keeper.
Part 1 - Reflection, Refraction and Snells Law
Law of reflection
When light strikes a mirror and reflects from its surface, the angle of reflection is equal to the angle of incidence, both angles being measured from the normal to the mirror surface. Also, the incident ray, the reflected ray and the normal to the surface all lie in the same plane.
Law of refraction (Snell's law)
When light passes from one transparent medium into another, in general the light will change speed at the interface between the two media. This change in speed is accompanied by a change in direction or refraction of the light. The angle through which the light changes direction depends on the angle of incidence at which the light strikes the surface and a characteristic of the media at the interface. This characteristic is known as the index of refraction, n, which is defined as
| $n = \dfrac{c_{vaccum}}{c_{medium}}$ | (1) |
where $c_{vacuum}$ is the speed of light in a vacuum and $c_{medium}$ is the speed of light in the medium.
The relationship between the direction of travel of light and the indices of refraction of the media is known as Snell's law,
| $n_1\sin\theta_1 = n_2\sin\theta_2$ | (2) |
where the angles $\theta_1$ and $\theta_2$ are measured between the light rays and the normal to the surface in each medium. You will verify Snell's law experimentally.
Measure the Index of Refraction of Water and Glass
For each index of refraction (both glass and water) perform the measurements for as many different angles as there are members in your group. This will ensure that everyone has a chance to make some of the physical measurements, and to provide a check on your measurement techniques. There is some judgement on the part of the experimenter as to exactly where to mark the lines which show the rays entering, passing through and leaving the object being measured. One way to test for consistency is to perform the measurement for multiple angles and with different people making the measurement.
- Find the index of refraction ($n$) for tap water.
- Find the index of refraction ($n$) for block glass.
- Using the piece of glass test whether or not the angle of reflection is equal to the angle of incidence.
 |
| Note the use of steel pins pressed into the cork board to hold both the laser and the glass (water tray) in place during the measurement. |
(Assume the index of refraction of air is 1.0).
Part 2 - Lenses, Images and Telescopes
Simple Lenses - focal point, focal length, and images
When reflecting or refracting materials like mirrors or clear glass are shaped in special ways, they can be used to re-direct light to form images. If the reflecting or refracting surfaces are spherical, this geometry (together with the laws of reflection and refraction) give rise to the ray diagrams illustrated in Fig 1. The lenses shown in Fig 1 are considered thin lenses for simplicity and it is assumed that all of the refraction takes place at the center of the lenses.
 |
| Figure 1: Parallel light rays entering from the left, striking lenses and mirrors, and continuing on. The focal points (fp) and focal lengths (f) are shown. |
Note that the double convex lens and the concave mirror of Figs. 1(a) and 1(b) redirect the light so that the light rays converge at the focal points. Images formed in this way are called real images, since light actually passes through them. Real images can be projected onto a screen.
Note also that the double concave lens and the convex mirror of Figs. 1(c) and 1(d) cause the rays to diverge. Images formed this way must be inferred by extending the light rays back to where they appear to have come from as the dashed lines show. Since no light actually passes through these images they are referred to as virtual images and they cannot be projected onto a screen.
The magnification of a lens or mirror is defined as the ratio of the image diameter to the object diameter.
The Lens Equation
A consequence of the laws of reflection and refraction and the spherical shape of the mirror or lens surface is the relationship
| $\dfrac{1}{f} = \dfrac{1}{OD} + \dfrac{1}{ID}$ | (3) |
where $f$ is the focal length, $OD$ is the object distance (the distance from the object to the lens or mirror), and $ID$ is the image distance (the distance from the lens or mirror to the image). It is remarkable that Eq. (3) applies both to mirrors and lenses with spherical surfaces even though the physics of refraction and reflection is quite different.
Measure the focal lengths of your lenses
Set up the apparatus as shown in Fig. 7.
 |
| Figure 7: Optical bench with light source, lens, and projection screen |
Use the lens makers equation and the apparatus provided to measure the focal lengths of your two lenses.
Note that the form of the lens makers equation suggests that you can make multiple independent measurements of the focal length of a lens, use this fact to make multiple measurements for each lens to check for consistency and to aid in assessing how well you know your final values.
Note that you need two lenses with different focal lengths for your telescope. One of your lenses should be about twice the focal length of the other. If your two lenses have the same focal length, one of your lenses has gotten mixed up with those of another group and you will need to figure out which group has one of your lenses and vice versa.
Telescope
Telescopes are optical instruments which create a magnified image of distant objects. The functional definition of a telescope can be stated as follows.
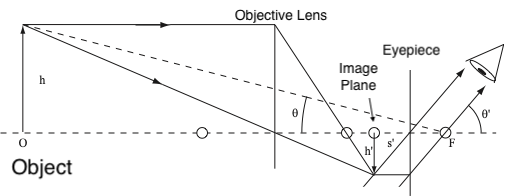
The objective lens creates an image of the object. The eyepiece is then positioned to magnify the image created by the objective lens. Figure 11 is a ray diagram of this statement.
 |
| Figure 11: (top) Telescope apparatus, (bottom) telescope magnification ray diagram |
The longer focal length lens will be the objective of your telescope while the shorter focal length lens will serve as the eyepiece.
Theoretically, for an object at infinity the magnification of a telescope should be the ratio of the focal lengths of the objective lens and the eye piece lens.
Construct a Telescope
The ray tracing diagram in Fig 11 presents a lot of information, but can be difficult to interpret. But if you study it for a bit, the function of the two lenses should become apparent.
- The purpose of the first lens (called the objective) is to create an image of a distant object. If the object is infinitely far from the objective its image will be located at focal point of the objective lens. Note that for objects closer than infinity the location of the image created by the objective lens will move slightly.
- The purpose of the second lens (called the eye piece) is to project the image created by the objective lens onto the lens of your eye.
Construct a telescope.
Using your longer focal length lens as the objective and the shorter focal length lens as the eye piece, construct a functional telescope on the optical rail.
- To make it easier to use the telescope, the eye piece should be placed near the end of one of the optical rails.
- You have a light source that can be used as an object to help work out the placement of the objective and eye piece lenses. This light source should be placed on a separate optical rail from the telescope so that it can be placed further away. Remember the assumption that the object you are observing is at or near infinity for an ideal telescope design. Having the light source further from the telescope will help approximate this condition.
- The translucent screen can be used to help establish the location of the image plane inbetween the objective and eye piece lenses.
- Keep in mind that when you look at an object through the telescope you will likely need to adjuse the position of the eye piece lens to achieve proper focus when observing objects at different distances.
Measure the Telescope Magnification
Once you have finished constructing your telescope work out a technique for measuring its magnification and compare this with the expected magnification calculated from the focal lengths of the lenses you use for the objective and the eye piece.
Point your telescope at a distant object. The building across the street as seen through a lab window is distant enough, an object at the far end of one of the two hall ways in Kersten would also be adequate. You may need to figure out a way to support one end of the telescope to get it pointing correctly, hand holding it will not work.
Your cell phone camera will be useful for measuring the magnification of a distant object. Think carefully about how this can be accomplished and come up with a step by step procedure that you can discuss with your TA. Some things to consider.
- What will you use as a distant object.
- How will you support the telescope.
- What are the important considerations for taking photos with your cell phone camera that will provide suitable data for measuring the magnification.
- How will you make measurements using your photos.
Once your TA approves your procedure go ahead and perform the measurement.
Report: Summary and Conclusions
After the lab, you will need to write up your conclusions. This should be a separate document, and it should be done individually (though you may talk your group members or ask questions).
The conclusion is your interpretation and discussion of your data. What do your data tell you? How do your data match the model (or models) you were comparing against, or to your expectations in general? Your conclusions should always be based on the results of your work in the lab. It is not acceptable to evaluate the results of an experiment by comparison to known values or any other form of preconceived expectation. Your conclusions need to be supported by your data. If your data are inconclusive or in disagreement with regard to your expectations then your conclusion should reflect that.
Make sure you cover the following points in your report.
Index of Refraction
- Describe your measured quantities, how you measured them and how you assessed their uncertainties. [EP][SC]
- Present your measurements appropriately. [SC]
- Show your calculations for the index of refraction of water and glass. [DA]
- Show your calculations for your test of the incident and reflected angles. [DA]
- Comment on whether or not your measured indices of refraction are consistent with expectations for water and borosilicate glass. [SC][DC]
Focal Length of Lenses
- Describe your measured quantities, how they were measured and how you assessed their uncertainties. [EP][SC]
- Present your measurements appropriately. [SC]
- Show your calculations for the focal lengths of your two lenses. [DA]
Telescope Magnification
- Describe how you chose to measure the magnification of your telescope. What object did you use and approximately how far away was it. How did you perform your measurements of the object with and without the telescope. [EP][SC]
- Show your calculations for both the theoretical and experimental values of the magnification. [DA]
- Compare your measured magnification to the theoretical value. [DC][SC]
REMINDER: Your report is due 48 hours after the lab. Submit a single PDF on Canvas.